Law of Conservation of Mass

All formulas are based on the physical nature of m=ρ×V (mass = density × volume)

Density value

Theoretical density of pure aluminum: 2,698 kg/m³ (20℃)

The approximate value of 2,700 kg/m³ is reasonable for industrial calculations (error < 0.1%)

2. Verification of the Rigorousness of Geometric Formulas

2.1. Standard geometric volume formula

2.2. In-depth verification of pipe formula

Square tube formula restrictions:

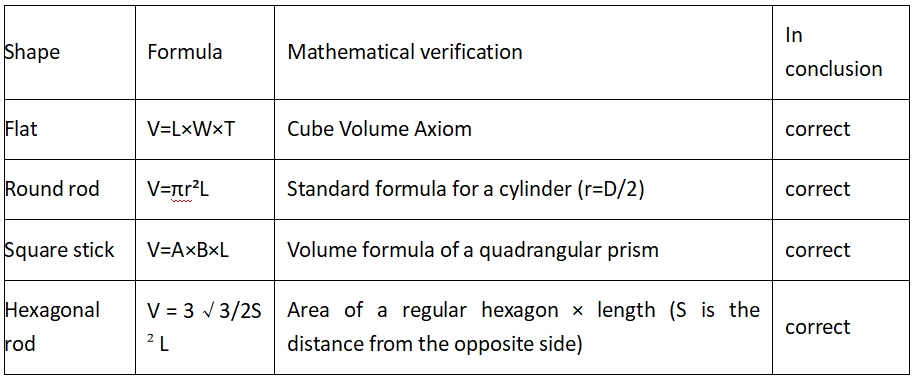
This is true when the tube wall thickness is uniform and the inner angle is a right angle (the actual square tube has a rounded transition, and the theoretical error is about 1-3%)

3. Unit System Consistency Verification

Cross-unit calculation risk point investigation

4. Engineering Suitability Amendment

4.1. Compensation for non-ideal factors

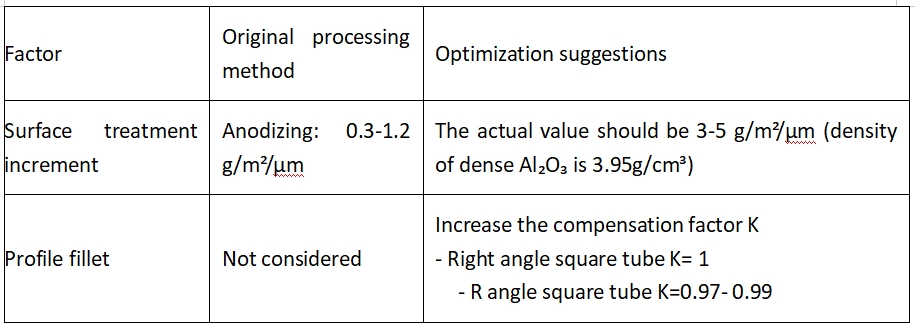
4.2. Quantification of tolerance impact

Thickness tolerance ±10% → Weight deviation ±(8% ~ 12%) (thin-walled parts are more sensitive)

Solution: W actual = W theoretical × (1 + Δt / t) ( Δt : thickness deviation)

5. Boundary Condition Test

Extreme case verification:

Density anomaly scenario

7xxx alloy (7075): Measured density 2.810 g/cm³ → If 2.7g/cm³ is used by mistake, the error is +4.1%.

Formula table

4t(A + B)- 4t² is a standard engineering calculation that is calculated by multiplying the perimeter of the section by the wall thickness and then deducting the four corners.

Calculation example:

1.6061 aluminum plate (1000 × 500 × 10 mm, length 2 m): W = 1000 × 500 × 2 × 0.0027 = 27 kg

2.7075 round tube (outer diameter 50 mm, wall thickness 3 mm, length 1.5 m): W = [(50-3)×3×3.1416×1.5]×0.00283 ≈ 5.65 kg

3. Square tube (40×40×2mm, length 3m): W = [2×2×(40+40-4)×3]×0.0027×0.98 ≈ 2.42 kg

Recommended Workflow

1. Select density → 2. Measure actual size → 3. Select compensation factor → 4. Calculate by formula